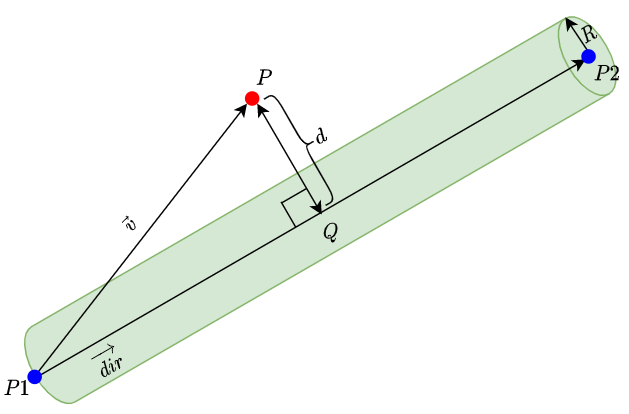
점 p는 실린더 내부에 있는가?
점 P가 실린더 내부에 있으려면
실린더 시작점과 끝점 사이에 있어야 한다.
실린더 축에서의 거리가 실린더 반경보다 작거나 같아야 한다.
위 두 조건을 만족해야 합니다.
첫 번째는 아래 식으로 검사할 수 있습니다.
\[\begin{align} P1 &= \text {실린더 시작점}\\ P2 &= \text {실린더 끝점}\\ R &= \text {실린더 반경}\\ dir &= \frac{\overrightarrow{P1 \to P2}}{|\overrightarrow{P1 \to P2}|} \quad \text{(}\overrightarrow{dir}\text{은 단위 벡터)}\\ v &= \overrightarrow{P1 \to P}\\ t &= \overrightarrow{dir} \cdot \vec{v} \quad \text{(t는 벡터의 내적 값)}\\ &=\begin{cases} t \ge 0 \text{ and } t \le |\overrightarrow{P1 \to P2}| \quad &\therefore \text{점 P는 실린더 시작점과 끝점 사이에 있음 }\\ otherwise \quad &\therefore \text{점 P는 실린더 외부에 존재} \end{cases} \end{align}\]점 P가 실린더의 시작점과 끝점 사이에 있다는 것을 알았다면
두 번째로 실린더 축과의 거리를 계산하여 실린더 반경($R$)보다 작은지 여부로 실린더 내부에 있는지 확인 할 수 있습니다.
\[\begin{align} Q &= P1 + \overrightarrow{dir}*t\\ d &= |Q \to P| \quad \text{Q에서 P까지의 거리}\\ &=\begin{cases} d \le R \quad &\therefore \text{점 P는 실린더 내부에 존재}\\ otherwise \quad &\therefore \text{실린더 외부에 존재} \end{cases} \end{align}\]위 식들을 코드로 작성하면 아래와 같습니다.
1
2
3
4
5
6
7
8
9
10
var dir = new Vector3D(P1, P2);
double length = dir.Length;
dir.Normalize();
var v = new Vector3D(P1, P);
double t = Vector3D.Dot(dir, v);
if(t < 0 || t > length) return false;
var Q = P1 + dir * t;
double d = Q.DistanceTo(P);
return (d <= R) ? true : false;