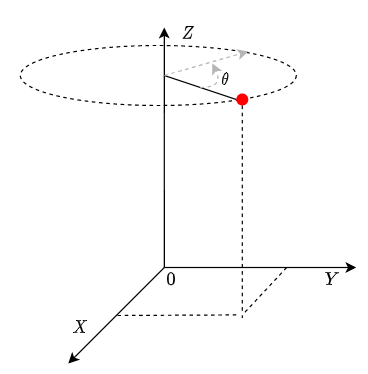
임의의 축에 대한 회전
원점을 기준으로 점 $(x,y,z)$을 $Z$축으로 $\theta$만큼 회전시키는 수식은 다음과 같이 행렬로 표현할 수 있습니다.
\[\begin{bmatrix} x'\\ y'\\ z' \end{bmatrix}= \begin{bmatrix} cos(\theta)& -sin(\theta)&0\\ sin(\theta)&cos(\theta)&0\\ 0&0&1 \end{bmatrix} * \begin{bmatrix} x\\ y\\ z \end{bmatrix}\]그리고 $X$ 혹은 $Y$ 축으로 회전한다면 행렬이 바뀌게 됩니다.
$X$축에 대한 회전 =
\[\begin{bmatrix} x'\\ y'\\ z' \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0\\ 0 & cos(\theta)& -sin(\theta) \\ 0&sin(\theta)&cos(\theta) \end{bmatrix} * \begin{bmatrix} x\\ y\\ z \end{bmatrix}\]$Y$축에 대한 회전 =
\[\begin{bmatrix} x'\\ y'\\ z' \end{bmatrix}= \begin{bmatrix} cos(\theta) & 0 & sin(\theta)\\ 0 & 1& 0 \\ -sin(\theta)&0&cos(\theta) \end{bmatrix} * \begin{bmatrix} x\\ y\\ z \end{bmatrix}\]좀더 일반적으로 점$(x,y,z)$을 임의의 축으로 회전하는 것을 생각해볼때 $X,Y,Z$축으로 회전하는 행렬로는 표현하기가 어렵습니다.
대부분의 3D Library에서는 축 회전에 대한 클래스를 제공하는데 eyeshot에서는 Rotation이 해당 클래스입니다. 아래는 점 $(x,y,z)$를 $Z$ 축으로 $\theta$ 만큼 회전하는 코드입니다.
1
2
3
var pos = new Vector3D(x,y,z);
var rotation = new Rotation(theta, Vector3D.AxisZ);
pos.Transformby(rotation);
$\overrightarrow{(1,1,1)}$ 축으로 회전하려면 아래와 같이 할 수 있습니다.
1
2
3
var pos = new Vector3D(x,y,z);
var rotation = new Rotation(theta, new Vector3D(1,1,1);
pos.Transformby(rotation);
이렇게 간결한 코드로 점$(x,y,z)$을 임의의 축으로 회전시킬 수 있습니다.